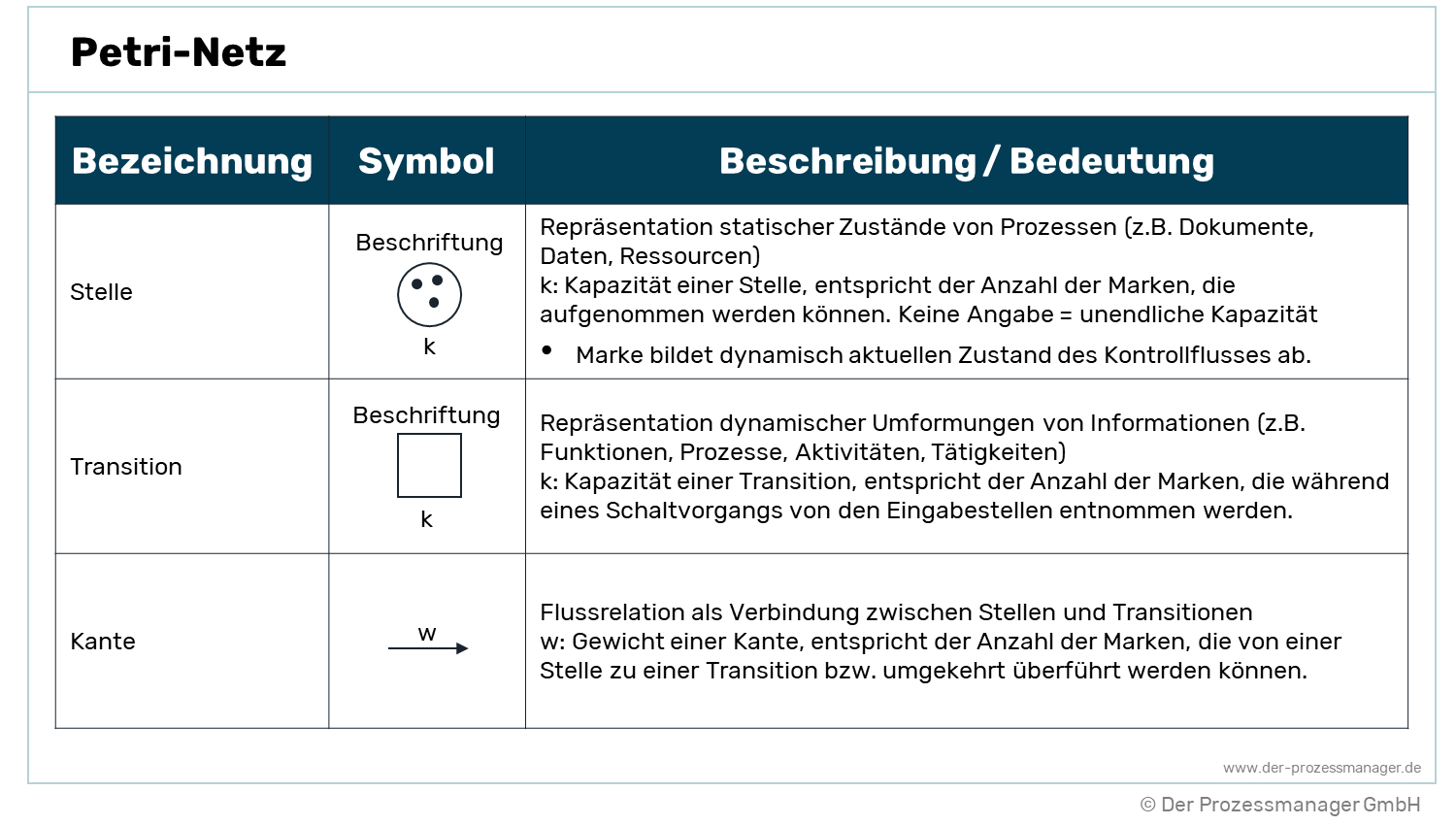
Ein Petri-Netz ist eine grafische Darstellung von Prozess-Zuständen in Form von Knoten und Kanten. Sie wird oft im Maschinenbau oder in der Logistik verwendet.
Ein Petri-Netz stellt eine grafische Darstellung von Prozess-Zuständen in Form von Knoten und Kanten dar. Die Kanten sind gerichtete Verbindungen der verschiedenen Knoten untereinander und stellen die ablauftechnischen Relationen zwischen den Knoten dar. Das Petri-Netz besteht aus zwei Arten von Knoten:
- Stellen (Kreise): Zustände, z.B. Dokumente, Daten und Ressourcen.
- Transistoren (Rechtecke): Transformation, z.B. Funktionen, Prozesse oder Aktivitäten.
In Petri-Netzen werden im Gegensatz zur Ereignisgesteuerten Prozesskette (EPK) keine Verknüpfungsoperatoren verwendet. Verknüpfungen werden implizit dargestellt. Um das dynamische Verhalten des Netzwerks darzustellen, werden Stellen mit sogenannten Marken belegt, die den aktuellen Zustand darstellen. Petri-Netze sind beliebt für die Simulation von Prozessen und Modellierung von Prozessen.
Ursprung und Entwicklung
Die Petrinetze stammen aus der Dissertation von Carl Adam Petri mit dem Titel “Kommunikation mit Automaten”. Petrinetze waren zunächst nur für Theoretiker interessant. Ab Mitte der 1980er Jahre wurden sie jedoch auch in der Praxis verwendet.
Seit den 1980er Jahren wurden verschiedene High-Level-Netz-Varianten mit Marken für Gegenstände, Daten oder Symbole vorgeschlagen. Diese Formalismen erhöhen die Ausdruckskraft von Platz-/Transitionsnetzen beträchtlich. Zugleich konnten viele Analysetechniken von Platz-/Transitionsnetzen auf diese Formalismen verallgemeinert werden.
Seit den 1980er Jahren gibt es viele neue Modellierungstechniken für verteilte Systeme und Algorithmen. Petri-Netze sind relevant und dienen oft als Maßstab für die Qualität und Ausdruckskraft von Modellen verteilter Systeme. Einen Überblick über zahlreiche Anwendungsbereiche von Petri-Netzen gibt.
Mit Petri-Netzen werden heutzutage Systeme modelliert, deren Verhalten aus diskreten, lokal begrenzten Schritten besteht. Das sind oft Systeme, die Rechner integrieren oder die mit Rechnern simuliert werden. Petri-Netze werden vielversprechend in der Systembiologie, Geschäftsprozessen und Service-orientierten Architekturen eingesetzt.
Eigenschaften
Nachfolgend findet man einige Eigenschaften von Petri-Netzen aufgeführt und kompakt erklärt.
Petri-Netz Tot
Von einer toten Transition unter einer Markierung m spricht man, wenn keine Folgemarkierung diese Transition aktivieren kann. Eine Markierung bezeichnet man hingegen als tot, wenn alle Transitionen tot sind.
Petri-Netz Lebendig
Lebendigkeit Petri-Netz: Eine Transition nennt man lebendig unter einer Markierung m, wenn sie unter keiner Folgemarkierung m‘ tot ist. Analog nennt man eine Markierung lebendig, wenn alle Transitionen lebendig sind.
Petri-Netz Verklemmungsfrei
Nicht ganz so streng nimmt es die Eigenschaft Verklemmungsfrei. Man nennt nämliche eine Markierung verklemmungsfrei, wenn keine tote Markierung erreichbar ist. Sollte der Markierungsgraph keinen Knoten ohne Nachfolge haben, dann ist das Netz verklemmungsfrei.
Petri-Netz Terminiert
Ist die Menge der Schaltfolgen eines markierten Petrinetzes endlich, dann terminiert das Petrinetz. Hat der Markierungsgraph keine Zyklen, dann ist das der Beweis, dass das Netz terminiert.
Petri-Netz Beschränkt
Bleibt die Anzahl der Marken in einem Petrinetz während der Laufzeit gleich, dann kann man von einem beschränkten Netz sprechen. Generell gilt ein Petrinetz als beschränkt, falls nicht unendlich viele Token erzeugt werden können.
Petri-NetzReversibel
Von einem reversiblen Netz spricht man, wenn die Startmarkierung m0 von jeder anderen erreichbaren Markierung aus erreichbar ist.
Petri-Netz Soundness
Ein Petri-Netz gilt als intakt (sound), wenn folgende drei Eigenschaften erfüllt sind:
- Für jede Markierung die in die Startstelle gelegt wird, muss es möglich sein, dass eine Markierung in der Endstelle entsteht
- Falls die Markierung die Endstelle erreicht, darf keine andere Stelle im Netz markiert sein
- Es darf keine tote Transitionen geben, alle Transitionen müssen vom initialen Zustand in einen Zustand kommen, in dem die Transition schalten kann
Free-Choice-Netz
Bei einem Free-Choice-Netz dürfen Transitionen einer vorwärts verzeigten Stelle nicht rückwärts verzweigt sein. Die Transitionen sind damit nur von der beteiligten Stelle abhängig und es kann „frei gewählt“ werden, welche Transition nun schalten soll. Es gibt also keine weitere Vorbedingung, die Wahl ist frei.
Vorteile und Nachteile von Petri-Netzen
Nachfolgend einige Vorteile und Nachteile von einfachen Petrinetzen:
Vorteile
- Formelle Syntax
- Einfach zu verstehen
- Gute Analysemöglichkeiten
- Hersteller unabhängig
Nachteile
- Modelle können groß und komplex werden
- Modelle werden schnell unüberschaubar
- Zeit, Kosten und Daten können nicht modelliert werden
Siehe auch:
Dokumente und Downloads:
- keine Dokumente zum Download verfügbar.
Literatur:
- Literatur Radar 2018 (zum Beitrag)
Quellen und Einzelnachweise
- Grundkurs Geschäftsprozessmanagement, Gadatsch (2012), S. 73f.
- Gabler: Petri-Netze
Weblinks:
- keine Weblinks bekannt.
Wissendatenbank-Partner und Autoren:
Autoren:
- Michael Durst (Xing-Profil)
- Sascha Hertkorn
- Christopher Eischer
- Nico Schweisser